تک قطبی مغناطیسی دیراک

چهار معادله نظریه الکترومغناطیس ماکسول که یکی از بزرگترین دستاوردهای تاریخ بشر است به نتایج مهمی انجامید. این معادلات دو پدیده الکتریسیته و مغناطیس را بهم ربط دادند و نشان دادند که الکتریسیته و مغناطیس تجلی های متفاوتی از الکترومغناطیس هستند، اما این معادلات یک محدودیت هم برای فیزیک در نظر می گیرند.

به گزارش بیگ بنگ، معادله دوم یعنی قانون مغناطیسی گوس، میگوید که چیزی بنام تک قطب مغناطیسی وجود ندارد. یعنی هرگز نمی توانید که قطب شمال را در یک دست و قطب جنوب را در دست دیگر داشته باشید. مغناطیسی که به دو نیمه می شود، دو مغناطیس تک قطبی ایجاد نمیکند، یعنی یکی با قطب شمال و دیگری با قطب جنوب، بلکه به دو مغناطیس دو قطبی تقسیم می شود. حتی اگر این عمل شکستن مغناطیس به دو تکه تا کوچک ترین ذره آن نیز ادامه یابد باز به دو قطب منجر می شود-قطب شمال و قطب جنوب.

اما از زمانی که فیزیکدان بزرگی بنام دیراک، وجود تک قطبی مغناطیسی را پیش گویی کرد، فیزیکدانان را به حیرت وا داشت. تک قطبی مغناطیسی ذره ای فرضی حامل یک بار مغناطیسی بنیادی است. در واقع یک تک قطب مغناطیسی شمال یا جنوب که مانند یک ذره آزاد رفتار می کند؛ این تک قطبی مغناطیسی شبیه بار الکتریکی است. دیراک می گفت که حتی اگر یک تک قطبی در جایی از عالم وجود داشته باشد، توضیح خواهد داد که چرا بار الکتریکی فقط به شکل مضربی از بار الکتریکی در الکترون وجود دارد. تاکنون هیچ کسی یک تک قطبی را مشاهده نکرده است، اما همین که در فیزیک انرژی بالا قلمروی جدید کشف می شود یا منبع جدید از ماده ظهور میکند تحقیق برای تک قطبی ها پا می گیرد.

یکی از مشکلات نظریه بیگ بنگ مربوط به تک قطبی های مغناطیسی است، طبق این نظریه باید اکنون تک قطبی های مغناطیسی به اندازه پروتون ها فراوان باشند ولی اینطور نیست. به گفته ی آلن گوث اگر جهان در حالتی از خلاء کاذب آغاز شده باشد، می تواند به صورت نمایی منبسط شود. در حالت خلاء کاذب، جهان می تواند ناگهان به مقدار غیر قابل تصوری متورم شود، که به موجب آن چگالی تک قطبی ها رقیق می شود. اگر دانشمندان تاکنون هیچ تک قطبی ندیده اند، تنها به این دلیل است که تک قطبی ها در سرتاسر جهانی پخش شده اند که از آنچه قبلا تصور می شد، بسیار بزرگتر است. گوث توانست معمای مشاهده نشدن تک قطبی ها را حل کند. براساس استدلال دیراک وجود تک قطبی مغناطیسی در جهان، ماهیت گسسته ی بار الکتریکی را توضیح می دهد. ایده ی دیراک فوق العاده اغوا گرایانه است، چراکه کوانتش باریکی از رمز آلودترین معماهای جهان فیزیکی است. اگر می خواهید جایزه نوبل را ببرید پس می دانید دنبال چه چیزی بگردید!

بزرگنمایی و معادلات عدسی

مقدمه

محاسبه مکان یک شیء و تصویر متناظر آن در عدسیها معمولا بدون رجوع به بزرگنمایی تصویر انجام می‌گیرد. هر چند ، در عمل هنگام ایجاد تصاویر حقیقی ، این  بزرگنمایی ، یعنی نسبت طول تصویر به طول جسم است که مشخص می‌کند تصویر ایجاد شده از نظر اندازه مناسب است یا خیر. همچنین ، اگر فاصله‌ها در محدوده فاصله کانونی و معادله به عنوان تابعی از بزرگنمایی نوشته شود. تخمینهای سریع یا فاصله کانونی و معادله به عنوان تابعی از بزرگنمایی نوشته شود. تخمینهای سریع یا محاسبات سر انگشتی و ذهنی معمولا سریعتر صورت می‌گیرند. 

بزرگنمایی

بزرگنمایی به صورت زیر تعریف می‌شود:

طول شیء / طول تصویر = M

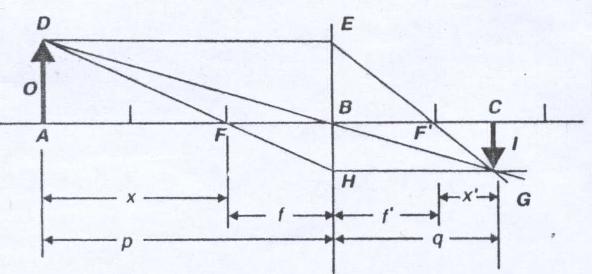
از تشابهات دو مثلث ABD و CBG حاصل از رسم پرتوهای فرودی و عبوری خواهیم داشت:(معادله 1)

M = I/O = q/p

از حالتهای بسیار رایج ، ثبت تصویر روی فیلمی به ابعاد 36×24 میلیمتر است. به عنوان مثال فرض کنید می‌خواهیم تصویر عمارت بلندی به طول 30 متر را روی یک فیلم 30 میلیمتری قرار دهیم. به عبارت دیگر ، بزرگنمایی باید چنین باشد:

M = I/O = 30/30000 mm = 1/1000

معادله گاوسی

رابطه بین شیء تا عدسی و تصویر تا عدسی برای عدسیهای نازک توسط کارل فردریش گاوس (1855-1777) در قرن نوزدهم ارائه گردید. این رابطه چنین است:(معادله 2)

f^-1 = 1/p + 1/q

که f فاصله کانونی عدسی p فاصله شیء تا عدسی p فاصله تصویر تا عدسی است. اما برای تخمین سریع یا محاسبه ذهنی ، شاید در این رابطه مقادیر معکوس زیاد مناسب نباشند. اگرمعادله (2) را در q ضرب کنیم، خواهیم داشت:(معادله 3)

q/f = q/p + q/q

q/r فاصله تصویر اندازه گیری شده برحسب فاصله کانونی q/p بزرگنمایی M و q/r برابر با 1 است. با جاگذاری q بجای q/r و M بجای q/p خواهیم داشت:(معادله 4)

Q = M +1

به عبارت دیگر ، فاصله تصویر (تا عدسی) ، (M+1) برابر فاصله کانونی است. به همین ترتیب می‌توانیم P یعنی فاصله شیء اندازه گیری شده بر حسب فاصله کانونی را چنین نمایش دهیم:

p = 1/M + 1

معادله نیوتن

در سالهای آغازین قرذن هجدهم ، ایزاک نیوتن (1727-1642) رابطه‌ای برای عدسیها نوشت که در آن فاصله شیء و تصویر نه عدسی بلکه دو کانون F و 'F اندازه گیری می‌شوند، همانطور که در شکل نشان داده شده است. نیوتن در کتاب "اپتیک" خود این رابطه را بدون توضیح چنین نوشته بود:

'x/f = f/x

وی در سالهای بعد استدلال کامل برای آن نیز ارائه داد. با مراجعه به شکل پیداست که این کمیتها مربوط به تشابه دو مثلث هستند. مثلثهای قائم الزاویه ADF و BHF باهم متشابهند. همین طور مثلثهای قائم الزاویه 'CGF و 'BEF نیز باهم متشابهند. از طرفی در شکل داریم: AD = BE = 0 و CG=BH=1 که نسبت تناسب آنها نیز توسط نیوتن ارائه شد. کتابهای درسی عصر حاضر ، این معادله را معمولا بصورت زیر می‌نویسند:(معادله 5)

'f² = xx

که می‌توان x و 'x را به ترتیب فاصله شیء تا کانون و تصویر تا کانون متناظر نامید. معادله نیوتن بیش از یک قرن ، پیشتر از معادله گاوس ارائه شده بود. در سالهای اخیر ، برخی کتابهای درسی این معادله را فقط بصورت یک تمرین مطرح می‌سازند و از دانش آموزان می‌خواهند که آن را از معادله گاوس بدست آورد، یا آنکه اصلا به آن اشاره‌ای نمی‌کنند. دو طرف معادله (5) را بر f² تقسیم می‌کنیم، خواهیم داشت:

1 = xx'/ff

که x/f و x'/f فاصله‌های جسم و تصویر بر حسب فاصله کانونی است. مناسب است که این عبارتها را به ترتیب با نمادهای x و 'x نمایش دهیم:(معادله 6)

'I = xx

معادله (6) نکته جالب و مفیدی را آشکار می‌سازد و آن این است که فاصله جسم برحسب فاصله کانونی ، x ، و فاصله تصویر برحسب فاصله کانونی ، 'x ، کمیتهایی هستند که با هم نسبت عکس دارند. از معادله‌های (3) و (4) می‌توان نوشت:(معادله 7)

q/f = M + 1

با جاگذاری ('f+x) برای q ، معادله (7) خواهد شد:

f + x')/f = M + 1)

پس از ساده شدن می شود:

1 + x'/f + 1 = M

x'/f = M

با جاگذاری 'x در سمت چپ معادله فوق ، خواهیم داشت:(معادله 8)

x' = M

می‌بینیم که معادله نیوتن برای عدسی می‌تواند از معادله گاوسی مناسبتر باشد، چون فاصله تصویر بر حسب فاصله کانونی از نظر عددی برابر با بزرگنمایی عدسی می‌شود. به همین ترتیب فاصله شیء بر حسب فاصله کانونی برابر عکس بزرگنمای می‌شود:(معادله 9)

x = 1/M

به مثال تصویر برداری از عمارت 30 متری برگردیم. تصویر در 1000/1 فاصله کانونی نسبت به کانون متناظر ، 'F و پشت عدسی تشکیل می‌شود. از آن سو ، شیء در 1000 برابر فاصله کانونی نسبت به کانون متناظر ، F ، جلوی عدسی قرار دارد. به عنوان مثالی دیگر ، دستگاه پروژکتور فیلم متحرک 355 میلیمتری را در نظر بگیرید. قاب تصویر 22×18 میلیمتر را اندازه می‌گیرد، اما برای پروژکتور به هنگام فیلمبرداری ابعاد فیلم 17.8×20.99 میلیمتر می‌شود. اگر فیلم بخواهد روی پرده‌ای به عرض 8 متر نمایش داده شود، در آن صورت بزرگنمایی تصویر خواهد شد: M = 8000/20.9 mm = 383

یعنی فاصله تصویر بر حسب فاصله کانونی 383 برابر فاصله کانونی تا پرده می‌شود. بنابراین ، می‌بینیم که بیان فاصله‌های جسم و تصویر (بر حسب کانونی) به عنوان تابعی از بزرگنمایی راهی سریع و مستقیم برای تجسم رابطه‌ها در معادلات عدسی است. معادله نیوتن ، بویژه ، کاربرد ساده و مفیدی را در این خصوص ارائه می‌دهد.

مباحث مرتبط با عنوان