بزرگنمایی و معادلات عدسی

مقدمه

محاسبه مکان یک شیء و تصویر متناظر آن در عدسیها معمولا بدون رجوع به بزرگنمایی تصویر انجام می‌گیرد. هر چند ، در عمل هنگام ایجاد تصاویر حقیقی ، این  بزرگنمایی ، یعنی نسبت طول تصویر به طول جسم است که مشخص می‌کند تصویر ایجاد شده از نظر اندازه مناسب است یا خیر. همچنین ، اگر فاصله‌ها در محدوده فاصله کانونی و معادله به عنوان تابعی از بزرگنمایی نوشته شود. تخمینهای سریع یا فاصله کانونی و معادله به عنوان تابعی از بزرگنمایی نوشته شود. تخمینهای سریع یا محاسبات سر انگشتی و ذهنی معمولا سریعتر صورت می‌گیرند. 

بزرگنمایی

بزرگنمایی به صورت زیر تعریف می‌شود:

طول شیء / طول تصویر = M

از تشابهات دو مثلث ABD و CBG حاصل از رسم پرتوهای فرودی و عبوری خواهیم داشت:(معادله 1)

M = I/O = q/p

از حالتهای بسیار رایج ، ثبت تصویر روی فیلمی به ابعاد 36×24 میلیمتر است. به عنوان مثال فرض کنید می‌خواهیم تصویر عمارت بلندی به طول 30 متر را روی یک فیلم 30 میلیمتری قرار دهیم. به عبارت دیگر ، بزرگنمایی باید چنین باشد:

M = I/O = 30/30000 mm = 1/1000

معادله گاوسی

رابطه بین شیء تا عدسی و تصویر تا عدسی برای عدسیهای نازک توسط کارل فردریش گاوس (1855-1777) در قرن نوزدهم ارائه گردید. این رابطه چنین است:(معادله 2)

f^-1 = 1/p + 1/q

که f فاصله کانونی عدسی p فاصله شیء تا عدسی p فاصله تصویر تا عدسی است. اما برای تخمین سریع یا محاسبه ذهنی ، شاید در این رابطه مقادیر معکوس زیاد مناسب نباشند. اگرمعادله (2) را در q ضرب کنیم، خواهیم داشت:(معادله 3)

q/f = q/p + q/q

q/r فاصله تصویر اندازه گیری شده برحسب فاصله کانونی q/p بزرگنمایی M و q/r برابر با 1 است. با جاگذاری q بجای q/r و M بجای q/p خواهیم داشت:(معادله 4)

Q = M +1

به عبارت دیگر ، فاصله تصویر (تا عدسی) ، (M+1) برابر فاصله کانونی است. به همین ترتیب می‌توانیم P یعنی فاصله شیء اندازه گیری شده بر حسب فاصله کانونی را چنین نمایش دهیم:

p = 1/M + 1

معادله نیوتن

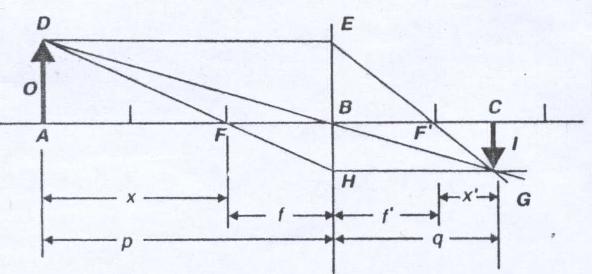
در سالهای آغازین قرذن هجدهم ، ایزاک نیوتن (1727-1642) رابطه‌ای برای عدسیها نوشت که در آن فاصله شیء و تصویر نه عدسی بلکه دو کانون F و 'F اندازه گیری می‌شوند، همانطور که در شکل نشان داده شده است. نیوتن در کتاب "اپتیک" خود این رابطه را بدون توضیح چنین نوشته بود:

'x/f = f/x

وی در سالهای بعد استدلال کامل برای آن نیز ارائه داد. با مراجعه به شکل پیداست که این کمیتها مربوط به تشابه دو مثلث هستند. مثلثهای قائم الزاویه ADF و BHF باهم متشابهند. همین طور مثلثهای قائم الزاویه 'CGF و 'BEF نیز باهم متشابهند. از طرفی در شکل داریم: AD = BE = 0 و CG=BH=1 که نسبت تناسب آنها نیز توسط نیوتن ارائه شد. کتابهای درسی عصر حاضر ، این معادله را معمولا بصورت زیر می‌نویسند:(معادله 5)

'f² = xx

که می‌توان x و 'x را به ترتیب فاصله شیء تا کانون و تصویر تا کانون متناظر نامید. معادله نیوتن بیش از یک قرن ، پیشتر از معادله گاوس ارائه شده بود. در سالهای اخیر ، برخی کتابهای درسی این معادله را فقط بصورت یک تمرین مطرح می‌سازند و از دانش آموزان می‌خواهند که آن را از معادله گاوس بدست آورد، یا آنکه اصلا به آن اشاره‌ای نمی‌کنند. دو طرف معادله (5) را بر f² تقسیم می‌کنیم، خواهیم داشت:

1 = xx'/ff

که x/f و x'/f فاصله‌های جسم و تصویر بر حسب فاصله کانونی است. مناسب است که این عبارتها را به ترتیب با نمادهای x و 'x نمایش دهیم:(معادله 6)

'I = xx

معادله (6) نکته جالب و مفیدی را آشکار می‌سازد و آن این است که فاصله جسم برحسب فاصله کانونی ، x ، و فاصله تصویر برحسب فاصله کانونی ، 'x ، کمیتهایی هستند که با هم نسبت عکس دارند. از معادله‌های (3) و (4) می‌توان نوشت:(معادله 7)

q/f = M + 1

با جاگذاری ('f+x) برای q ، معادله (7) خواهد شد:

f + x')/f = M + 1)

پس از ساده شدن می شود:

1 + x'/f + 1 = M

x'/f = M

با جاگذاری 'x در سمت چپ معادله فوق ، خواهیم داشت:(معادله 8)

x' = M

می‌بینیم که معادله نیوتن برای عدسی می‌تواند از معادله گاوسی مناسبتر باشد، چون فاصله تصویر بر حسب فاصله کانونی از نظر عددی برابر با بزرگنمایی عدسی می‌شود. به همین ترتیب فاصله شیء بر حسب فاصله کانونی برابر عکس بزرگنمای می‌شود:(معادله 9)

x = 1/M

به مثال تصویر برداری از عمارت 30 متری برگردیم. تصویر در 1000/1 فاصله کانونی نسبت به کانون متناظر ، 'F و پشت عدسی تشکیل می‌شود. از آن سو ، شیء در 1000 برابر فاصله کانونی نسبت به کانون متناظر ، F ، جلوی عدسی قرار دارد. به عنوان مثالی دیگر ، دستگاه پروژکتور فیلم متحرک 355 میلیمتری را در نظر بگیرید. قاب تصویر 22×18 میلیمتر را اندازه می‌گیرد، اما برای پروژکتور به هنگام فیلمبرداری ابعاد فیلم 17.8×20.99 میلیمتر می‌شود. اگر فیلم بخواهد روی پرده‌ای به عرض 8 متر نمایش داده شود، در آن صورت بزرگنمایی تصویر خواهد شد: M = 8000/20.9 mm = 383

یعنی فاصله تصویر بر حسب فاصله کانونی 383 برابر فاصله کانونی تا پرده می‌شود. بنابراین ، می‌بینیم که بیان فاصله‌های جسم و تصویر (بر حسب کانونی) به عنوان تابعی از بزرگنمایی راهی سریع و مستقیم برای تجسم رابطه‌ها در معادلات عدسی است. معادله نیوتن ، بویژه ، کاربرد ساده و مفیدی را در این خصوص ارائه می‌دهد.

مباحث مرتبط با عنوان

آب سنگین و نحوه ی تولید و مصرف آن

اب سنگین- چگونگی تولید و موارد مصرف آن

آب سنگین چیست؟
آب سنگین، آبی است که هیدروژن های آن دوتریوم یا ایزوتوپ سنگین هیدروژن است. این آب در مقایسه با آب معمولی نقطه جوش و نقطه انجماد بالاتری دارد و ویسکوزیته یا چسبندگی آن بیشتر است. هیدروژن دارای 2 ایزوتوپ پایدار H و D و یک ایزوتوپ ناپایدار و رادیواکتیو T یا تریتیوم است. هسته ایزوتوپ معمولی هیدروژن دارای یک پروتون و هسته ایزوتوپ سنگین دارای یک پروتون و یک نوترون است. این نوترون اضافی، هم سبب کاهش جذب نوترون توسط دوتریوم در آب سنگین می شود و هم افزایش جرم آن را به همراه دارد. جرم ملکولی آب معمولی 18 و آب سنگین 20 است. در نتیجه یک لیتر آب سنگین دارای جرمی بیشتر از یک لیتر آب سبک است.

 آب سنگین چگونه تولید می شود؟
محققان برای اولین بار به طریق الکترولیز (برقکافت) به آب سنگین خالص دست یافتند. چون نقطه جوش آب سنگین بالاتر از آب معمولی است، برای تولید آن، از روش تبخیر و تقطیر هم استفاده می شود. در تأسیسات تولید آب سنگین در اراک، طی مراحلی پیچیده از آب معمولی، آب سنگین به دست می آید که درجه خلوص آن 99/8 درصد است. تفاوت جرم آب سنگین و آب سبک قابل ملاحظه است و تفاوت در نقاط جوش این 2 نوع آب، امکان جداسازی آب سنگین و خالص سازی آن را تسهیل می کند. از میان هر 6400 تا 7000 ملکول آب معمولی، یک ملکول آب سنگین وجود دارد که برای دستیابی به آن از طرق فیزیکی و شیمیایی درجه خلوص آن را بالا می برند ، تأسیسات تولید آب سنگین تاکنون فقط در 8 کشور وجود داشته است که ما نهمین کشور هستیم.

کاربرد آب سنگین:

بیشترین استفاده ازآب سنگین درراکتورها است که شامل هر2 راکتور تحقیقاتی و نیروگاهی می شود
نیروگاه هایی که از انرژی شکافت اورانیوم استفاده می کنند به 2 بخش نیروگاه آب سبک و آب سنگین تقسیم می شوند. نیروگاه آب سبک دارای راکتور آب سبک و نیروگاه آب سنگین دارای راکتور آب سنگین است. سوخت نیروگاه های هسته ای، اورانیوم 238 و 235 است. اگر از اورانیوم 235 به عنوان سوخت هسته ای استفاده شود باید درجه غنای آن از 7/ 0 درصد (که در طبیعت وجود دارد) به 3 تا 5 درصد برسد تا جرم بحرانی لازم برای شکافت را داشته باشد. درون یک راکتور هسته ای، اورانیوم توسط نوترون ها، بمباران می شود. برخورد نوترون به هسته اتم اورانیوم، سبب شکست آن می شود و در اثر این شکست، انرژی و نوترون های اضافی به وجود می آید. نوترون های اضافی در یک واکنش زنجیره ای شرکت می کنند و باعث شکست دیگر اتم های اورانیوم می شود. اگر این نوترون های اضافی کنترل نشود، ورود آن ها به واکنش های زنجیره ای، سبب تولید انرژی بسیار زیاد و در نتیجه انفجار در راکتور می شود. از شکست هسته هر اتم اورانیوم معادل 200 میلیون الکترون ولت انرژی آزاد می شود؛ بنابراین باید از موادی که جاذب نوترون های اضافی هستند و یا کندکننده ها، استفاده شود. در راکتورهای آب سبک از اورانیوم 235 به عنوان سوخت و از آب سبک یا معمولی به عنوان کندکننده استفاده می شود. در راکتورهای آب سنگین، از اورانیوم معمولی یا 238 به عنوان سوخت و از آب سنگین برای کند کردن واکنش های زنجیره ای، بهره گرفته می شود. اگر در راکتور آب سنگین، از آب معمولی استفاده کنیم تمامی نوترون های حاصل از شکافت، توسط آب جذب شده و واکنش زنجیره ای متوقف می شود، درحالی که آب سنگین توانایی کمی در جذب نوترون دارد. پس از شکست هسته اورانیوم 235 یا 238، انرژی به صورت گرمایی آزاد و این انرژی توسط مواد خنک کننده و به منظور به حرکت درآوردن توربین به خارج از راکتور منتقل می شود. این مواد خنک کننده می تواند آب معمولی یا آب سنگین باشد که پس از انتقال حرارت به بیرون از راکتور و خنک شدن، مجددا" به راکتور برمی گردد و این فرآیند به صورت پیوسته، برای تولید برق، ادامه پیدا می کند. بنابراین آب سنگین و آب سبک در راکتورها علاوه بر کندکنندگی، نقش خنک کنندگی هم دارند.
از آب سنگین برای تولید رادیوایزوتوپ ها در صنعت، کشاورزی و پزشکی استفاده می شود همچنین در رادیوگرافی، نوترون تراپی و نوترون رادیوگرافی از آن بهره برداری می شود. علاوه براین ها، آب سنگین برای تشخیص نشت آب های زیرزمینی یا نشت آب از سدها، کاربرد زیادی دارد. باتوجه به این که کشور ما دارای منابع بزرگی از اورانیوم طبیعی است، با تولید آب سنگین در اراک، می توانیم راکتورهای آب سنگینی بسازیم که برای سوخت خود نیازی به کار دشوار و پرهزینه غنی سازی اورانیوم ندارند. در تأسیسات اراک سالانه 16 تن آب سنگین تولید می شود که نه تنها در تولید برق از نیروگاه های آب سنگین کاربرد دارد، بلکه مصارف زیادی در پزشکی هسته ای دارد. همان طور که ذکر شد از آب سنگین برای تولید رادیوایزوتوپ ها و رادیوداروها استفاده می شود. رادیوایزوتوپ ها در صنعت و کشاورزی کاربرد زیادی دارند. پروژه تولید آب سنگین در اراک به اندازه دستیابی به فرآیند غنی سازی اورانیوم افتخارآفرین است.
به گفته دکتر نورانی متخصص پزشکی هسته ای اساس کار در دانش پزشکی هسته ای استفاده از رادیوایزوتوپ ها و رادیوداروها است و از آب سنگین می توان به عنوان تارگت نوترون برای تولید این مواد استفاده کرد. از پرتوداروها برای تشخیص و درمان بیماری هایی چون سرطان، تومورهای خوش خیم و بدخیم، نارسایی های قلبی و عروقی استفاده می شود. مثلا" در پت اسکن که پیشرفته ترین تکنیک در پزشکی هسته ای است، گلوکز نشان دار یا FDG یا فلوئودین کاربرد بسیار زیادی دارد برای نشان دار کردن گلوکز از آب سنگین استفاده می شود که به عنوان مثال از FDG برای بررسی متابولیسم گلوکز و تشخیص تومورها در مغز بهره گیری می شود.

باتوجه به این که واردات بعضی رادیوایزوتوپ ها و رادیوداروها از کشورهای دیگر با مشکل مواجه است، تولید آب سنگین در کشور موفقیت بزرگی چه در عرصه تولید برق و چه در عرصه پزشکی و صنعت و کشاورزی محسوب می شود.

اگر ماه نباشد چه اتفاقی برای زمین می افتد؟

ماه همواره یکی از مهم‌ترین مؤلفه‌های سازنده در ایجاد شرایط مناسب برای تکامل حیات در سیاره ما به شمار می‌رفته است، اما یافته‌های علمی اخیر نشان می‌دهد زمین آن قدرها هم که تصور می‌شده وابسته به وجود ماه نیست.

به گزارش بیگ بنگ به نقل از جام جم، ژاک لاسکار، ستاره شناس فرانسوی در سال ۱۹۹۳ با انجام محاسبات پیچیده ریاضی به این نتیجه رسید که وجود گرانش ماه در ثابت نگه داشتن انحراف محوری زمین حیاتی است. انحراف محوری زمین در تعیین الگوی آب و هوایی نقش بسیار مهمی دارد و اگر دائم در حال تغییر باشد باعث بروز یک شرایط آب و هوایی بشدت متغیر می شود که تبعات زیست محیطی آن آرامش ساکنان زمین را مختل خواهد کرد.

لاسکار معتقد است ما زمینی ها بسیار خوش اقبال هستیم که قمری به این بزرگی بالای سرمان در آسمان داریم. هیچ کدام از سیاره های سنگی منظومه شمسی از این موهبت برخوردار نیستند. مریخ یا همان سیاره سرخ دو ماه کوچک دارد که با نام های فوبوس و دِیموس شناخته می شوند. اینها در واقع سیارک هایی بوده اند که در مدار مریخ به دام افتاده و البته تأثیر چندانی روی مریخ ندارند. از این رو، انحراف محوری مریخ میلیون ها سال است که مرتباً تغییر می کند و حتی گاهی انحراف محور چرخشی آن به بزرگی حداقل ۴۵ درجه می رسد. اما این خوش اقبالی زمینی ها در داشتن یک ماه منحصر به فرد فقط حاصل یک اتفاق بود. ۴٫۵ میلیارد سال پیش، یک سیاره یا سیارک عظیم (تقریباً به اندازه مریخ) با زمین برخورد کرد و از خرده سنگ های حاصل از این انفجار مهیب، ماه شکل گرفت. بر اساس فرضیه زمین کمیاب، پیتر وارد و دونالد براونلی در کتابی با همین عنوان استدلال کردند که فقط در سیاره های بسیار معدودی همه چیز برای تکامل حیات مهیاست. حال یافته های اخیر حاکی از آن است که باید در تحلیل های پیشین شک کرد.

جک لیسوئر از مرکز تحقیقات آمِس ناسا، جیسن بارنز از دانشگاه آیداهو و جان چمبرز از مؤسسه علوم کارنِگی به اتفاق نشان دادند که اگر ماه نبود چه اتفاقی برای زمین می افتاد. پژوهشگران دریافتند در صورت نبود ماه فقط ده درجه به انحراف فعلی محور چرخشی زمین که ۲۳٫۵ درجه است، اضافه خواهد شد. به نظر می رسد لاسکار در محاسبات خود دچار اشتباه شده بود. کامپیوترهای عصر جدید سریع تر و پرقدرت تر از ماشین های محاسباتی دهه ۱۹۹۰ عمل می کنند و می توانند نتایج دقیق تری ارائه دهند. پژوهشگران گفته اند که اگر زمین سریع تر می چرخید، مثلاً این که طول یک شبانه روز کمتر از ده ساعت می شد یا جهت چرخش زمین برعکس می شد، یعنی این که خورشید از مغرب طلوع و در مشرق غروب می کرد، آن وقت زمین می توانست از نیروی گرانشی سایر سیارات به ویژه مشتری استفاده کند و دیگر نیازی به ماه نداشت.

زمین هر ۲۴ ساعت یک بار به دور خود می چرخد. بعد از اتفاقی که به شکل گیری ماه منجر شد، زمین هر چهار یا پنج ساعت یک بار به دور خود می چرخید. اما سرعت چرخش آن به علت وجود ماه بتدریج کم شد. سرعت چرخش زمین پیش از شکل گیری ماه هنوز مشخص نیست، اما گمان می رود که حرکت سریعی داشته و حتی گاهی جهت چرخش آن عوض می شده است. در زمان پیدایش زمین این برخورد اجرام سنگین بود که بر جهت چرخش آن اثر گذاشت.

پژوهشگران معتقدند که جهت چرخش بیشتر سیارات سنگی از غرب به شرق است، اما عده دیگری اظهار می کنند بعضی سیارات سنگی در هر دو جهت می چرخند و این یعنی تعداد سیاراتی که جهت چرخش آنها از شرق به غرب است کم نیست. پژوهشگران نتیجه گرفتند که حیات در سیارات سنگی به وجود ماه وابسته نیست. حتی در بعضی موارد وجود یک ماه بزرگ می تواند تبعات زیست محیطی فاجعه بار داشته باشد. یافته های اخیر موقعیت جدیدی را برای اختر زیست شناسان فراهم کرده تا در جستجوی سکونتگاه های فرازمینی به موقعیت های جدیدتری فکر کنند.

-